Comparaison entre les relations force-vitesse du sprint non-chargé et du sprint-résisté avec traîneau : méthodes d'essai simple vs multiples.
Introduction :
L'évaluation de la production d'énergie est courante dans la pratique des sciences du sport (Cross et al., 2017b, Jaric, 2015).
En plus d'évaluer simplement la production d'énergie pendant un mouvement explosif donné, il est possible de mieux comprendre les capacités des athlètes en mesurant l'expression de la production de force sur une gamme de vitesses [c.-à-d. la relation la force-vitesse (Fv)] (Morin et Samozino 2016). En pratique, les relations Fv sont généralement évaluées selon l'une des deux méthodes suivantes :
Cependant, en dehors de la quantification de la charge, on ne sait pas encore si les capacités mécaniques évaluées à l'aide d'une méthode de sprints multiples et d'une seule méthode de sprint présente des caractéristiques similaires.
Il est généralement reconnu dans le domaine de l'entraînement en résistance que l’entrainement en fonction de la relation Fv ou de ses dérivés (ex. entrainement basé sur la vitesse (Scott et al., 2016)), fournit un moyen efficace de cibler les adaptations (Cormie et al., 2011, Morin et Samozino, 2016).
Cependant, le corps de la littérature actuelle examinant les effets de la résistance au sprint est quelque peu limité, et utilise généralement des charges relativement légères (Petrakos et al., 2016).
Le but de cette étude était de comparer les relations Fv déterminées par plusieurs sprints avec résistance à celles déterminées à partir d'un seul essai de sprint non chargé. Plus précisément, nous avons cherché à savoir si le sprint avec une charge donnée à un effort maximal pouvait modéliser les conditions cinétiques externes rencontrées pendant une portion particulière d'une phase de sprint non chargée (c'est-à-dire correspondant à la même vitesse).
Un objectif secondaire était d'examiner si des paramètres pratiques de résistance au sprint résistants pouvaient être déterminés à partir d'un seul sprint, rendant inutile la réalisation de plusieurs essais.
Méthodes
Sujets et protocole
Les données utilisées pour cette étude ont été compilées à partir d'un groupe d'athlètes masculins (n = 27) utilisés pour prouver le concept de relations force-vitesse-puissance de sprint avec traîneau (Cross et coll., 2017b).
Après un protocole d'échauffement détaillé, les athlètes ont effectué 6 ou 7 sprints de sprints avec un traîneau chargé d'une sélection de masses sur une piste d'athlétisme. Le test a été précédé d’un repos passif de 5 minutes, de même entre les séries.
Équipement
Pour fournir la résistance, les athlètes ont été attachés à un traîneau de sprint pour poids lourds (5,64 kg ; HT 50 mm traîneau, Auckland, NZL) chargé avec une sélection de poids calibrés. La performance de sprint a été mesurée par un pistolet radar sportif (modèle m: Stalker ATS II, Applied Concepts, Dallas, TX, USA), fixé à un trépied placé à 5 m derrière la ligne de départ et d'une hauteur de 1 m.
Sélection de charges et distance de sprint
Sept paramètres résistifs (six charges externes et une condition « déchargée ») ont été réalisés pour fournir une gamme suffisante de stimuli afin de favoriser la production d’un pic d’énergie. Après un sprint non chargé, la charge a été augmentée par tranche de 20% de poids de corps (Body Mass = BM) (jusqu'à 120% de BM) jusqu'à une diminution d'environ 50% de la vitesse maximale déchargée (c'est-à-dire vmax) et un pic visuel de puissance. Les sprints ont été effectués sur une piste d'athlétisme intérieure marquée, selon les distances préétablies suivantes : 45 m déchargés ; 40 m à 20% de BM ; 30 m à 40% de BM ; 30 m à 60% de BM ; 30 m à 80% de BM ; 20 m à 100% de BM ; et 20 m à 120% BM.
Relations force-vitesse et puissance-vitesse et conditions de charge optimales
Les relations Fv et Pv ont été générées pour un athlète individuel en utilisant des méthodes d'essais simples et multiples.
Dans le cas de la méthode d'essai unique, elle était composée de valeurs instantanées tout au long de l'accélération (Samozino et al., 2016).
Pour la méthode de sprint multiples, des valeurs uniques de chaque variable ont été obtenues pour chaque sprint afin de compiler une seule relation. (Lakomy 1987). F0, v0 et SFv ont été déterminés en tant qu'interceptions graphiques des relations Fv et de la pente de régression (respectivement). Pmax a été déterminé comme le sommet des relations Pv quadratiques en utilisant la première dérivation mathématique de l'équation quadratique associée. Les conditions optimales de puissance (vopt et Fopt) ont été calculées au point de Pmax, correspondant à 0,5·v0 et 0,5·F0.
Lopt a été calculé de la même manière pour les deux essais, en utilisant un calcul inverse pour déterminer la charge normale du traîneau correspondant au pic de la relation Pv (c'est-à-dire vopt et Fopt). En pratique, le Lopt final présenterait une résistance horizontale égale à Fopt (en combinaison avec Faero), et une vitesse de résistance maximale égale à vopt ; le résultat est un sprint où la vitesse maximale est atteinte dans les conditions précises de Pmax, représenté graphiquement comme le pic de la courbe Pv (voir Fig. 1).
Introduction :
L'évaluation de la production d'énergie est courante dans la pratique des sciences du sport (Cross et al., 2017b, Jaric, 2015).
En plus d'évaluer simplement la production d'énergie pendant un mouvement explosif donné, il est possible de mieux comprendre les capacités des athlètes en mesurant l'expression de la production de force sur une gamme de vitesses [c.-à-d. la relation la force-vitesse (Fv)] (Morin et Samozino 2016). En pratique, les relations Fv sont généralement évaluées selon l'une des deux méthodes suivantes :
- Essais répétés contre plusieurs conditions d'augmentation de la résistance externe (méthode des essais multiples)
- Ou pendant un seul essai d'accélération cyclique (méthode d'essai unique) (Cross et all 2017b).
Cependant, en dehors de la quantification de la charge, on ne sait pas encore si les capacités mécaniques évaluées à l'aide d'une méthode de sprints multiples et d'une seule méthode de sprint présente des caractéristiques similaires.
Il est généralement reconnu dans le domaine de l'entraînement en résistance que l’entrainement en fonction de la relation Fv ou de ses dérivés (ex. entrainement basé sur la vitesse (Scott et al., 2016)), fournit un moyen efficace de cibler les adaptations (Cormie et al., 2011, Morin et Samozino, 2016).
Cependant, le corps de la littérature actuelle examinant les effets de la résistance au sprint est quelque peu limité, et utilise généralement des charges relativement légères (Petrakos et al., 2016).
Le but de cette étude était de comparer les relations Fv déterminées par plusieurs sprints avec résistance à celles déterminées à partir d'un seul essai de sprint non chargé. Plus précisément, nous avons cherché à savoir si le sprint avec une charge donnée à un effort maximal pouvait modéliser les conditions cinétiques externes rencontrées pendant une portion particulière d'une phase de sprint non chargée (c'est-à-dire correspondant à la même vitesse).
Un objectif secondaire était d'examiner si des paramètres pratiques de résistance au sprint résistants pouvaient être déterminés à partir d'un seul sprint, rendant inutile la réalisation de plusieurs essais.
Méthodes
Sujets et protocole
Les données utilisées pour cette étude ont été compilées à partir d'un groupe d'athlètes masculins (n = 27) utilisés pour prouver le concept de relations force-vitesse-puissance de sprint avec traîneau (Cross et coll., 2017b).
Après un protocole d'échauffement détaillé, les athlètes ont effectué 6 ou 7 sprints de sprints avec un traîneau chargé d'une sélection de masses sur une piste d'athlétisme. Le test a été précédé d’un repos passif de 5 minutes, de même entre les séries.
Équipement
Pour fournir la résistance, les athlètes ont été attachés à un traîneau de sprint pour poids lourds (5,64 kg ; HT 50 mm traîneau, Auckland, NZL) chargé avec une sélection de poids calibrés. La performance de sprint a été mesurée par un pistolet radar sportif (modèle m: Stalker ATS II, Applied Concepts, Dallas, TX, USA), fixé à un trépied placé à 5 m derrière la ligne de départ et d'une hauteur de 1 m.
Sélection de charges et distance de sprint
Sept paramètres résistifs (six charges externes et une condition « déchargée ») ont été réalisés pour fournir une gamme suffisante de stimuli afin de favoriser la production d’un pic d’énergie. Après un sprint non chargé, la charge a été augmentée par tranche de 20% de poids de corps (Body Mass = BM) (jusqu'à 120% de BM) jusqu'à une diminution d'environ 50% de la vitesse maximale déchargée (c'est-à-dire vmax) et un pic visuel de puissance. Les sprints ont été effectués sur une piste d'athlétisme intérieure marquée, selon les distances préétablies suivantes : 45 m déchargés ; 40 m à 20% de BM ; 30 m à 40% de BM ; 30 m à 60% de BM ; 30 m à 80% de BM ; 20 m à 100% de BM ; et 20 m à 120% BM.
Relations force-vitesse et puissance-vitesse et conditions de charge optimales
Les relations Fv et Pv ont été générées pour un athlète individuel en utilisant des méthodes d'essais simples et multiples.
Dans le cas de la méthode d'essai unique, elle était composée de valeurs instantanées tout au long de l'accélération (Samozino et al., 2016).
Pour la méthode de sprint multiples, des valeurs uniques de chaque variable ont été obtenues pour chaque sprint afin de compiler une seule relation. (Lakomy 1987). F0, v0 et SFv ont été déterminés en tant qu'interceptions graphiques des relations Fv et de la pente de régression (respectivement). Pmax a été déterminé comme le sommet des relations Pv quadratiques en utilisant la première dérivation mathématique de l'équation quadratique associée. Les conditions optimales de puissance (vopt et Fopt) ont été calculées au point de Pmax, correspondant à 0,5·v0 et 0,5·F0.
Lopt a été calculé de la même manière pour les deux essais, en utilisant un calcul inverse pour déterminer la charge normale du traîneau correspondant au pic de la relation Pv (c'est-à-dire vopt et Fopt). En pratique, le Lopt final présenterait une résistance horizontale égale à Fopt (en combinaison avec Faero), et une vitesse de résistance maximale égale à vopt ; le résultat est un sprint où la vitesse maximale est atteinte dans les conditions précises de Pmax, représenté graphiquement comme le pic de la courbe Pv (voir Fig. 1).
Résultats
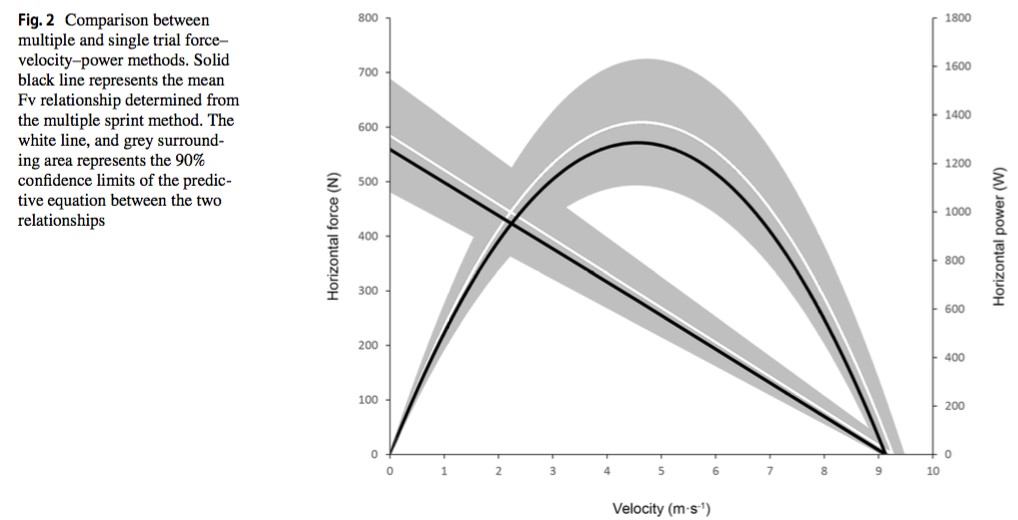
Le biais relatif moyen entre les méthodes se situait entre - 6,4 et - 0,4% (vers la méthode du sprint unique). Les mesures basées sur la vélocité étaient les plus appariées (corrélations très fortes), avec peu de biais (- 1,4 et - 0,4%) et de faibles niveaux d'erreur. Tout en présentant de fortes corrélations, les mesures de la force et de la puissance présentaient des niveaux d'erreur importants entre les approches. La figure 2 présente une représentation graphique de la comparaison des profils Fv obtenus à partir des deux méthodes.
Le biais relatif moyen entre les méthodes se situait entre - 6,4 et - 0,4% (vers la méthode du sprint unique). Les mesures basées sur la vélocité étaient les plus appariées (corrélations très fortes), avec peu de biais (- 1,4 et - 0,4%) et de faibles niveaux d'erreur. Tout en présentant de fortes corrélations, les mesures de la force et de la puissance présentaient des niveaux d'erreur importants entre les approches. La figure 2 présente une représentation graphique de la comparaison des profils Fv obtenus à partir des deux méthodes.
Discussion
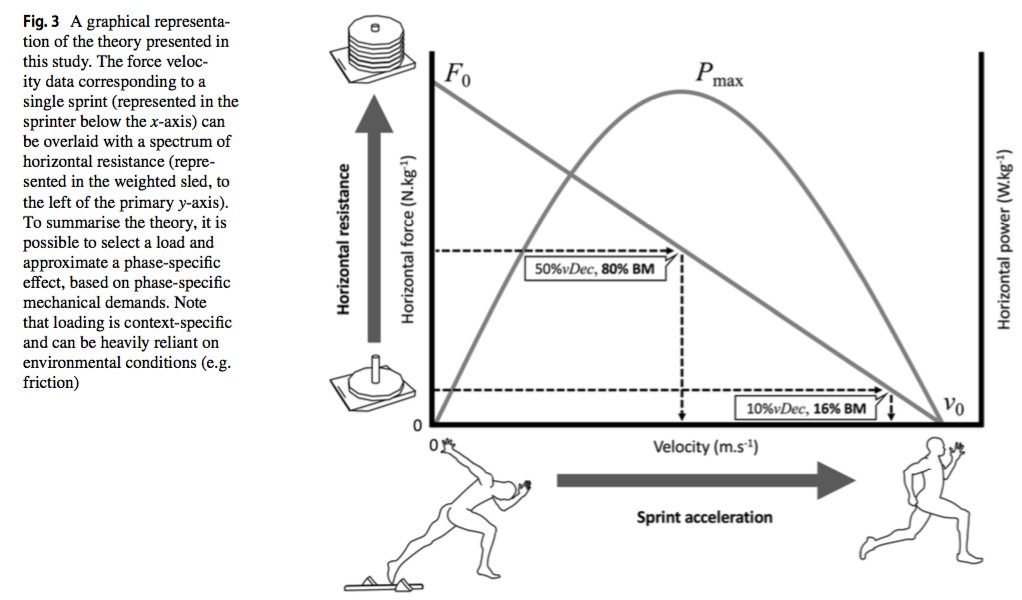
La conclusion la plus importante et la plus pratique de cette expérience est la forte association générale entre les relations composites déterminées par le sprint libre et les essais de sprint multiples avec résistance (r = 0,71 à 0,99). Bien que l'erreur existe, les relations développées à partir de chaque méthode sont typiquement similaires. Bien que ce résultat soit attendu par l’ensemble de la littérature sur les méthodes d'essais multiples versus simples en cyclismes (Driss et Vandewalle 2013), à notre connaissance l'interaction entre les deux méthodes n'a pas été testée ou discutée en sprint. En pratique, maintenir un effort de sprint maximal avec une charge résistive donnée peut reproduire les conditions rencontrées lors d'un essai de sprint non résisté, associées à la section relative de la relation Fv (voir la figure 3 pour une représentation graphique). Dans l'exemple d'un athlète tractant un Lopt individualisé (par exemple ~ 82% BM), le sprint dans ces conditions imite le moment où la puissance est maximisée pendant un sprint non chargé (c.-à-d. après 2-3 pas, ou dans une accélération précoce (Rabita et al., 2015)). Ces résultats fournissent la preuve qu'une section de la phase d'accélération de sprint peut potentiellement être ciblée et améliorée en fonction de la prescription de charges individualisées à partir de la relation Fv (Jimenez-Reyes et al., 2016) ; mais avec l'hypothèse d'une certaine inexactitude due à une erreur et potentiellement un transfert 'direct' réduit lors de l'utilisation de protocoles de charges plus importantes. En conséquence, l'entraînement effectué dans une condition de charge de sprint avec résistance peut être transféré à des adaptations spécifiques à la phase de sprint libre non chargé. Il est important de noter que si cette théorie met en évidence que les charges très lourdes (qui étaient auparavant réprimées (Alcaraz et al., 2009)) peuvent être prometteuses dans le développement de la force horizontale maximale ou de la puissance à faible vitesse (début de sprint) (Cross et al 2017b, Morin et al., 2017), les charges plus légères traditionnellement utilisées dans la recherche (ou même les méthodes « assistées ») ont probablement un intérêt dans le développement de la force horizontale à haute vitesse – dans le développement de « la vitesse pure », de la « vélocité » des athlètes (Morin et al.,
2012).
La conclusion la plus importante et la plus pratique de cette expérience est la forte association générale entre les relations composites déterminées par le sprint libre et les essais de sprint multiples avec résistance (r = 0,71 à 0,99). Bien que l'erreur existe, les relations développées à partir de chaque méthode sont typiquement similaires. Bien que ce résultat soit attendu par l’ensemble de la littérature sur les méthodes d'essais multiples versus simples en cyclismes (Driss et Vandewalle 2013), à notre connaissance l'interaction entre les deux méthodes n'a pas été testée ou discutée en sprint. En pratique, maintenir un effort de sprint maximal avec une charge résistive donnée peut reproduire les conditions rencontrées lors d'un essai de sprint non résisté, associées à la section relative de la relation Fv (voir la figure 3 pour une représentation graphique). Dans l'exemple d'un athlète tractant un Lopt individualisé (par exemple ~ 82% BM), le sprint dans ces conditions imite le moment où la puissance est maximisée pendant un sprint non chargé (c.-à-d. après 2-3 pas, ou dans une accélération précoce (Rabita et al., 2015)). Ces résultats fournissent la preuve qu'une section de la phase d'accélération de sprint peut potentiellement être ciblée et améliorée en fonction de la prescription de charges individualisées à partir de la relation Fv (Jimenez-Reyes et al., 2016) ; mais avec l'hypothèse d'une certaine inexactitude due à une erreur et potentiellement un transfert 'direct' réduit lors de l'utilisation de protocoles de charges plus importantes. En conséquence, l'entraînement effectué dans une condition de charge de sprint avec résistance peut être transféré à des adaptations spécifiques à la phase de sprint libre non chargé. Il est important de noter que si cette théorie met en évidence que les charges très lourdes (qui étaient auparavant réprimées (Alcaraz et al., 2009)) peuvent être prometteuses dans le développement de la force horizontale maximale ou de la puissance à faible vitesse (début de sprint) (Cross et al 2017b, Morin et al., 2017), les charges plus légères traditionnellement utilisées dans la recherche (ou même les méthodes « assistées ») ont probablement un intérêt dans le développement de la force horizontale à haute vitesse – dans le développement de « la vitesse pure », de la « vélocité » des athlètes (Morin et al.,
2012).
Conclusions et applications pratiques
• La charge optimale approximative peut être déterminée à partir d'un seul sprint, à condition que les caractéristiques du coefficient de frottement de l'essai et de la surface d'entraînement soient connues. De plus, la vitesse optimale déterminée à partir d'un seul sprint peut avoir une application valable sur d'autres modalités de sprint résisté (par exemple les sprints isocinétiques).
• La résistance légère (par exemple ~ 10% de diminution de vmax) fournit probablement un stimulus efficace pour le développement de la force horizontale à des vitesses élevées. Cependant, un entrainement utilisant des protocoles de charges plus élevés (par exemple une diminution de > 50% de vmax) peut fournir une surcharge plus efficace pour le développement de performances de sprint de courte distance (c'est-à-dire force et puissance maximum).
• La cause de l'augmentation de l'erreur entre les méthodes justifie une enquête plus approfondie. Jusqu'à cette date, les lecteurs sont priés d'interpréter les conditions mécaniques rencontrées au cours du sprint comme mécaniquement similaires, mais pas identiques.
Article original : Matt R. Cross · Pierre Samozino · Scott R. Brown· Jean-Benoît Morin A comparison between the force–velocity relationships of unloaded and sled-resisted sprinting: single vs. multiple trial methods European Journal of Applied Physiology https://doi.org/10.1007/s00421-017-3796-5
Mots clés : Performance explosive, Sprint, Développement de la puissance, Sprints résistés
Références
Alcaraz PE, Palao JM, Elvira JL (2009) Determining the optimal load for resisted sprint training with sled towing. J Strength Cond Res 23:480–485. https://doi.org/10.1519/JSC.0b013e318198f92c
Arsac LM, Locatelli E (2002) Modeling the energetics of 100-m running by using speed curves of world champions. J Appl Physiol (1985) 92:1781–1788. https://doi.org/10.1152/ japplphysiol.00754.2001
Cormie P, McCaulley GO, Triplett NT, McBride JM (2007) Optimal loading for maximal power output during lower-body resist- ance exercises. Med Sci Sports Exerc 39:340–349. https://doi. org/10.1249/01.mss.0000246993.71599.bf
Cormie P, McGuigan MR, Newton RU (2011) Developing maximal neuromuscular power: Part 2—training considerations for improv- ing maximal power production. Sports Med 41:125–146. https:// doi.org/10.2165/11538500-000000000-00000
Cross MR, Brughelli M, Samozino P, Brown SR, Morin JB (2017a) Optimal loading for maximising power during sled-resisted sprint- ing. Int J Sports Physiol Perform:1–25 https://doi.org/10.1123/ ijspp.2016-0362
Cross MR, Brughelli M, Samozino P, Morin JB (2017b) Methods of power–force–velocity profiling during sprint running: a nar- rative. Rev Sports Med 47:1255–1269. https://doi.org/10.1007/ s40279-016-0653-3
Cross MR, Tinwala F, Lenetsky S, Samozino P, Brughelli M, Morin JB (2017c) Determining friction and effective loading for sled sprinting. J Biomech 35:2198–2203. https://doi.org/10.1080/02 640414.2016.1261178
Driss T, Vandewalle H (2013) The measurement of maximal (anaero- bic) power output on a cycle ergometer: a critical review. Biomed Res Int 2013:589361. https://doi.org/10.1155/2013/589361
Hopkins WG, Marshall SW, Batterham AM, Hanin J (2009) Progres- sive statistics for studies in sports medicine and exercise sci- ence. Med Sci Sports Exerc 41:3–13. https://doi.org/10.1249/ MSS.0b013e31818cb278
Jaric S (2015) Force–velocity relationship of muscles perform- ing multi-joint maximum performance tasks. Int J Sports Med 36:699–704. https://doi.org/10.1055/s-0035-1547283
Jaric S (2016) Two-load method for distinguishing between muscle force, velocity, and power-producing capacities. Sports Med. https://doi.org/10.1007/s40279-016-0531-z
Jaskólska A, Goossens P, Veenstra B, Jaskólskp A, Skinner JS (1998) Treadmill measurement of the force–velocity relationship and power output in subjects with different maximal running velocities. Sports Med Training Rehab 8:347–358. https://doi. org/10.1080/15438629909512537
Jimenez-Reyes P, Samozino P, Brughelli M, Morin JB (2016) Effec- tiveness of an individualized training based on force–veloc- ity profiling during jumping. Front Physiol 7:677. https://doi. org/10.3389/fphys.2016.00677
Kawamori N, Haff GG (2004) The optimal training load for the devel- opment of muscular power. J Strength Cond Res 18:675–684. https://doi.org/10.1519/1533-4287(2004)18<675:TOTLFT>2.0 .CO;2
Lakomy HKA (1987) The use of a non-motorized treadmill for ana- lysing sprint performance. Ergonomics 30:627–637. https://doi. org/10.1080/00140138708969756
Lockie RG, Murphy AJ, Spinks CD (2003) Effects of resisted sled tow- ing on sprint kinematics in field-sport athletes. J Strength Cond Res 17:760–767. https://doi.org/10.1016/s1440-2440(02)80129-3
Morin JB, Samozino P (2016) Interpreting power-force-velocity pro- files for individualized and specific training. Int J Sports Physiol Perform 11:267–272. https://doi.org/10.1123/ijspp.2015-0638
Morin JB, Samozino P, Bonnefoy R, Edouard P, Belli A (2010) Direct measurement of power during one single sprint on treadmill. J Biomech 43:1970–1975. https://doi.org/10.1016/j. jbiomech.2010.03.012
Morin JB, Bourdin M, Edouard P, Peyrot N, Samozino P, Lacour JR (2012) Mechanical determinants of 100-m sprint running performance. Eur J Appl Physiol 112:3921–3930. https://doi. org/10.1007/s00421-012-2379-8
Morin JB et al (2015) Acceleration capability in elite sprinters and ground impulse: push more, brake less? J Biomech 48:3149–3154. https://doi.org/10.1016/j.jbiomech.2015.07.009
Morin JB, Petrakos G, Jimenez-Reyes P, Brown SR, Samozino P, Cross MR (2017) Very-heavy sled training for improving hori- zontal force output in soccer players. Int J Sports Physiol Perform 12:840–844. https://doi.org/10.1123/ijspp.2016-0444
Petrakos G, Morin JB, Egan B (2016) Resisted sled sprint training to improve sprint performance: a systematic. Rev Sports Med 46:381–400. https://doi.org/10.1007/s40279-015-0422-8
Rabita G, Dorel S, Slawinski J, Sàez-de-Villarreal E, Couturier A, Samozino P, Morin JB (2015) Sprint mechanics in world-class athletes: a new insight into the limits of human locomotion. Scand J Med Sci Sports
Samozino P, Rabita G, Dorel S, Slawinski J, Peyrot N, Saez de Vil- larreal E, Morin JB (2016) A simple method for measuring power, force, velocity properties, and mechanical effectiveness in sprint running. Scand J Med Sci Sports 26:648–658. https:// doi.org/10.1111/sms.12490
Scott BR, Duthie GM, Thornton HR, Dascombe BJ (2016) Training monitoring for resistance exercise. Theory Appl Sports Med 46:687–698. https://doi.org/10.1007/s40279-015-0454-0
Soriano MA, Jimenez-Reyes P, Rhea MR, Marin PJ (2015) The optimal load for maximal power production during lower-body resistance exercises: a meta-analysis. Sports Med 45:1191–1205. https://doi. org/10.1007/s40279-015-0341-8
Spinks CD, Murphy AJ, Spinks WL, Lockie RG (2007) The effects of resisted sprint training on acceleration performance and kin- ematics in soccer, rugby union, and Australian football players. J Strength Cond Res 21:77–85. https://doi.org/10.1519/R-18145.1
van Ingen Schenau GJ, Jacobs R, de Koning JJ (1991) Can cycle power predict sprint running performance? Eur J Appl Physiol Occup Physiol 63:255–260. https://doi.org/10.1007/bf00233857
Vandewalle H, Peres G, Heller J, Panel J, Monod H (1987) Force– velocity relationship and maximal power on a cycle ergometer: correlation with the height of a vertical jump. Eur J Appl Physiol Occup Physiol 56:650–656. https://doi.org/10.1007/bf00424805
Wilson GJ, Newton RU, Murphy AJ, Humphries BJ (1993) The opti- mal training load for the development of dynamic athletic perfor- mance. Med Sci Sports Exerc 25:1279–1286
• La charge optimale approximative peut être déterminée à partir d'un seul sprint, à condition que les caractéristiques du coefficient de frottement de l'essai et de la surface d'entraînement soient connues. De plus, la vitesse optimale déterminée à partir d'un seul sprint peut avoir une application valable sur d'autres modalités de sprint résisté (par exemple les sprints isocinétiques).
• La résistance légère (par exemple ~ 10% de diminution de vmax) fournit probablement un stimulus efficace pour le développement de la force horizontale à des vitesses élevées. Cependant, un entrainement utilisant des protocoles de charges plus élevés (par exemple une diminution de > 50% de vmax) peut fournir une surcharge plus efficace pour le développement de performances de sprint de courte distance (c'est-à-dire force et puissance maximum).
• La cause de l'augmentation de l'erreur entre les méthodes justifie une enquête plus approfondie. Jusqu'à cette date, les lecteurs sont priés d'interpréter les conditions mécaniques rencontrées au cours du sprint comme mécaniquement similaires, mais pas identiques.
Article original : Matt R. Cross · Pierre Samozino · Scott R. Brown· Jean-Benoît Morin A comparison between the force–velocity relationships of unloaded and sled-resisted sprinting: single vs. multiple trial methods European Journal of Applied Physiology https://doi.org/10.1007/s00421-017-3796-5
Mots clés : Performance explosive, Sprint, Développement de la puissance, Sprints résistés
Références
Alcaraz PE, Palao JM, Elvira JL (2009) Determining the optimal load for resisted sprint training with sled towing. J Strength Cond Res 23:480–485. https://doi.org/10.1519/JSC.0b013e318198f92c
Arsac LM, Locatelli E (2002) Modeling the energetics of 100-m running by using speed curves of world champions. J Appl Physiol (1985) 92:1781–1788. https://doi.org/10.1152/ japplphysiol.00754.2001
Cormie P, McCaulley GO, Triplett NT, McBride JM (2007) Optimal loading for maximal power output during lower-body resist- ance exercises. Med Sci Sports Exerc 39:340–349. https://doi. org/10.1249/01.mss.0000246993.71599.bf
Cormie P, McGuigan MR, Newton RU (2011) Developing maximal neuromuscular power: Part 2—training considerations for improv- ing maximal power production. Sports Med 41:125–146. https:// doi.org/10.2165/11538500-000000000-00000
Cross MR, Brughelli M, Samozino P, Brown SR, Morin JB (2017a) Optimal loading for maximising power during sled-resisted sprint- ing. Int J Sports Physiol Perform:1–25 https://doi.org/10.1123/ ijspp.2016-0362
Cross MR, Brughelli M, Samozino P, Morin JB (2017b) Methods of power–force–velocity profiling during sprint running: a nar- rative. Rev Sports Med 47:1255–1269. https://doi.org/10.1007/ s40279-016-0653-3
Cross MR, Tinwala F, Lenetsky S, Samozino P, Brughelli M, Morin JB (2017c) Determining friction and effective loading for sled sprinting. J Biomech 35:2198–2203. https://doi.org/10.1080/02 640414.2016.1261178
Driss T, Vandewalle H (2013) The measurement of maximal (anaero- bic) power output on a cycle ergometer: a critical review. Biomed Res Int 2013:589361. https://doi.org/10.1155/2013/589361
Hopkins WG, Marshall SW, Batterham AM, Hanin J (2009) Progres- sive statistics for studies in sports medicine and exercise sci- ence. Med Sci Sports Exerc 41:3–13. https://doi.org/10.1249/ MSS.0b013e31818cb278
Jaric S (2015) Force–velocity relationship of muscles perform- ing multi-joint maximum performance tasks. Int J Sports Med 36:699–704. https://doi.org/10.1055/s-0035-1547283
Jaric S (2016) Two-load method for distinguishing between muscle force, velocity, and power-producing capacities. Sports Med. https://doi.org/10.1007/s40279-016-0531-z
Jaskólska A, Goossens P, Veenstra B, Jaskólskp A, Skinner JS (1998) Treadmill measurement of the force–velocity relationship and power output in subjects with different maximal running velocities. Sports Med Training Rehab 8:347–358. https://doi. org/10.1080/15438629909512537
Jimenez-Reyes P, Samozino P, Brughelli M, Morin JB (2016) Effec- tiveness of an individualized training based on force–veloc- ity profiling during jumping. Front Physiol 7:677. https://doi. org/10.3389/fphys.2016.00677
Kawamori N, Haff GG (2004) The optimal training load for the devel- opment of muscular power. J Strength Cond Res 18:675–684. https://doi.org/10.1519/1533-4287(2004)18<675:TOTLFT>2.0 .CO;2
Lakomy HKA (1987) The use of a non-motorized treadmill for ana- lysing sprint performance. Ergonomics 30:627–637. https://doi. org/10.1080/00140138708969756
Lockie RG, Murphy AJ, Spinks CD (2003) Effects of resisted sled tow- ing on sprint kinematics in field-sport athletes. J Strength Cond Res 17:760–767. https://doi.org/10.1016/s1440-2440(02)80129-3
Morin JB, Samozino P (2016) Interpreting power-force-velocity pro- files for individualized and specific training. Int J Sports Physiol Perform 11:267–272. https://doi.org/10.1123/ijspp.2015-0638
Morin JB, Samozino P, Bonnefoy R, Edouard P, Belli A (2010) Direct measurement of power during one single sprint on treadmill. J Biomech 43:1970–1975. https://doi.org/10.1016/j. jbiomech.2010.03.012
Morin JB, Bourdin M, Edouard P, Peyrot N, Samozino P, Lacour JR (2012) Mechanical determinants of 100-m sprint running performance. Eur J Appl Physiol 112:3921–3930. https://doi. org/10.1007/s00421-012-2379-8
Morin JB et al (2015) Acceleration capability in elite sprinters and ground impulse: push more, brake less? J Biomech 48:3149–3154. https://doi.org/10.1016/j.jbiomech.2015.07.009
Morin JB, Petrakos G, Jimenez-Reyes P, Brown SR, Samozino P, Cross MR (2017) Very-heavy sled training for improving hori- zontal force output in soccer players. Int J Sports Physiol Perform 12:840–844. https://doi.org/10.1123/ijspp.2016-0444
Petrakos G, Morin JB, Egan B (2016) Resisted sled sprint training to improve sprint performance: a systematic. Rev Sports Med 46:381–400. https://doi.org/10.1007/s40279-015-0422-8
Rabita G, Dorel S, Slawinski J, Sàez-de-Villarreal E, Couturier A, Samozino P, Morin JB (2015) Sprint mechanics in world-class athletes: a new insight into the limits of human locomotion. Scand J Med Sci Sports
Samozino P, Rabita G, Dorel S, Slawinski J, Peyrot N, Saez de Vil- larreal E, Morin JB (2016) A simple method for measuring power, force, velocity properties, and mechanical effectiveness in sprint running. Scand J Med Sci Sports 26:648–658. https:// doi.org/10.1111/sms.12490
Scott BR, Duthie GM, Thornton HR, Dascombe BJ (2016) Training monitoring for resistance exercise. Theory Appl Sports Med 46:687–698. https://doi.org/10.1007/s40279-015-0454-0
Soriano MA, Jimenez-Reyes P, Rhea MR, Marin PJ (2015) The optimal load for maximal power production during lower-body resistance exercises: a meta-analysis. Sports Med 45:1191–1205. https://doi. org/10.1007/s40279-015-0341-8
Spinks CD, Murphy AJ, Spinks WL, Lockie RG (2007) The effects of resisted sprint training on acceleration performance and kin- ematics in soccer, rugby union, and Australian football players. J Strength Cond Res 21:77–85. https://doi.org/10.1519/R-18145.1
van Ingen Schenau GJ, Jacobs R, de Koning JJ (1991) Can cycle power predict sprint running performance? Eur J Appl Physiol Occup Physiol 63:255–260. https://doi.org/10.1007/bf00233857
Vandewalle H, Peres G, Heller J, Panel J, Monod H (1987) Force– velocity relationship and maximal power on a cycle ergometer: correlation with the height of a vertical jump. Eur J Appl Physiol Occup Physiol 56:650–656. https://doi.org/10.1007/bf00424805
Wilson GJ, Newton RU, Murphy AJ, Humphries BJ (1993) The opti- mal training load for the development of dynamic athletic perfor- mance. Med Sci Sports Exerc 25:1279–1286



 Entrainement de sprints avec traineau chargé : Comment déterminer la charge optimale ?
Entrainement de sprints avec traineau chargé : Comment déterminer la charge optimale ?





